Machine Learning for Different Resolution Pictures
The article describes modern methods for image super-resolution based on machine learning. The most used methods of this class are theoretically analyzed; their main advantages and disadvantages are outlined. A number of practical experiments were conducted to increase the resolution of images of different classes. Based on both the visual evaluation of the received images and the evaluation using the PSNR, a comparison was made between the efficiency of the various methods. The expediency of using one method or another for various tasks related to the previous processing of images are substantiates. The results of practical experiments are presented.
Keywords: image super-resolution, machine learning, convolution neural network, geometric transformation model
ANN, artificial neural network; NLS, neural-like structure; GTM, geometric transformation model; CNN, convolution neural network; HR, high resolution; LR, low resolution; PSNR, peak signal to noise ratio.
The task of providing super-resolution is a task, which is mainly formulated in the inverse form and is solved by the method or a set of methods for preserving the finest details of an image by processing one input image or a set of input images of one scene. The image super-resolution is provided due to an increase in the number pixels per unit area in the original sample. Similar methods for the case of one input image are based on reconstruction or learning. Other methods, in the case of a set of images of one scene, use additional normatively based on the sub pixel offset on the non-target pixel value in the middle of the set. The purpose of the work is to study and compare single-frame image super-resolution techniques.
Methods for providing image super-resolution, when processing one image, can be divided into two main groups (Figure 1): on the basis of reconstruction and on the basis of learning.1 The purpose of the images super-resolution methods based on the technology of reconstruction is to restore image details due to the interpolation of the input sample of low resolution (LR) while maintaining the sharpness of the edges of the image. Varieties of such algorithms are quite numerous.2,3 Despite the satisfactory results of the images super-resolution methods based on reconstruction, a number of shortcomings characterizes them. In particular, at resolution increases, the contours of objects on the image become homogeneous, lubricated, which results in the unnatural appearance of the image. Their performance depends on the used a priori information and its compatibility with the given images. In addition, these methods require post-processing.
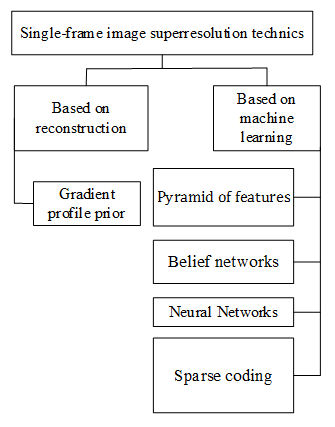
Figure 1 Classification of the single-frame image super-resolution techniques.
Image super-resolution techniques based on the machine learning: theoretical comparison
Image super-resolution methods based on learning include creating a training model to determine the correspondences between low and high resolution images, which are usually set from the database (images with a high resolution (HR) focus object are predominantly given, and low-resolution images are created by reducing sampling rate or thinness). The procedure for securing super-resolution is to apply the obtained "trained" model for reconstruction of HR images from the LR input sample. Various methods of this class restore the missing details on the resulting image using the similarity between the input sample of LR and examples in the training set.1 Learning methods can work in two ways. The first is the pixel approach, where each value in the resulting HR image is obtained by processing adjacent pixels using statistical training. Such processing may be based on weighted average adjacent pixels. Methods of this approach are characterized by efficiency in removing lubricants and muffling the image.4 Another approach is the framing.5 It involves evaluating the relationships between low and high resolution frames. It is used to restore the most likely frames in the resulting image based on the frames of the input LR sample. The effectiveness of such procedures depends to a great extent on the quality, and in some cases, on the size of the training sample. Therefore, the main task of the methods of this group is to solve the problem of forming effective pairs of learning frames of low / high resolution images.
Methods of image super-resolution based on pyramid of features are described in papers.6–8 Statistical models of these methods include the construction of three bottom-up pyramids based on the input image: Gauss, Laplace, and pyramid peculiarities (local texture measures) according to the procedures presented in.7 Gauss's pyramid is formed by scrolling the image and applying a digitization algorithm with a factor of 2 at each level and is used to construct the other two pyramids. The lower levels of the Laplace's pyramid are considered as high-frequency components of the original image. That is why the resulting HR image is formed by adding images of the Gauss and Laplace pyramids of one level. The multilevel representation of the image allows you to construct non-parametric learning from the ratio of the set of pixels of the pyramid of singularities and Laplace between two adjacent levels using the L2 metric. Because of such a system, for the test image, the most probable HR image (frames) is searched for among the relevant samples from all pyramids. Sometimes, the method of closest neighboring value is used to solve this problem. Given the low speed of these methods,7 a tree-like structure is used to find the most probable sample (frame). However, the results of their work are characterized by distortion of some regions of the resulting image. In order to reduce the manifestation of this disadvantage,8 developed a modified scheme of the methods of this approach. This idea is also based on the properties of self-similarity between frames of images, presented in the form of pyramids. However, these methods use only one pyramid to build a training sample. In Congyong,8 Gauss's pyramid is built and contextual-limited segmentation of the image and level is used to form a learning sample from frames of different context categories. In Datsenko6 clustering is used for this. The same idea is also used in, Liu7 but instead of the Gaussian pyramid, they construct a three-level Laplace pyramid here. The relationships between low/high resolution frames for all three methods are established on the basis of the reference vector method. Other methods of this group are based on similar approaches, but a number of shortcomings characterize them all. Obviously, the multi-level representation of the image, also in the form of several pyramids, is accompanied by the use of a large amount of computing resources. In addition, the learning process can be very slow, and the prediction of the expected frames is not always accurate. In addition, the complex probabilistic models of this class method do not take into account global constraints. This leads to the fact that some of the global properties of the object of attention on the image, such as explicit contours, the coherence of illumination and symmetry are missed.
Another area of methods for providing HR images – methods based on sparse representation (sparse coding).9,10 They use the assumption that each frame from the target image can be represented (sparse decomposition) using a linear combination of several elements of the training sample. In other words, each frame from the target image is generated by multiplying the elements of the training sample into sparse vectors of the coefficients. This assumption made it possible to develop a training sample based on the study of pairs of images for a rare image reconstruction,9 which later became known as the Yang's method. Further development of the methods of this class consisted in reducing the working time of such procedures and improving the quality of the original images. For this purpose, a method10 (Zeyde's method) has been developed, which uses the reduction of dimension by using the method of Analysis of the Main Component and the K-SVD algorithm and the Orthogonal Matching Pursuit-for learning the dictionary. The described class of methods greatly reduces the number of training selections to small "dictionaries" with larger properties to generalization, but their optimization requires the use of a sparse decomposition procedure, which may not be a trivial task. In addition, these methods produce sharp boundaries of output frames of HR images, which affect the overall quality of the synthesized image.
The use of belief networks such as Markovian networks or tree-like structures for the task of providing super-resolution is described in.11,12 According to the procedure of these methods, a pair of low / high resolution images is split into frames. For the corresponding frames, two functions are calculated: the observation function and the transition function.12 The observation function is used to evaluate how precisely the HR candidate frame corresponds to the LR frame, and the transition function evaluates the accuracy of matching between the HR candidate frame and its neighbor. The training model of these methods uses the belief propagation algorithm on the Markov random field. Its purpose is to produce the most probable HR frame, linking it to each known LR frame in such a way that adjoining areas are compatible with each other. In the training and deduction, a hidden Markov model is used to factorize the a posteriori probability. The main disadvantage of the methods of this group is that they show satisfactory results only with small coefficients of increase of resolution.11,12 The concept of neural network methods for images super-resolution is similar to the concept of methods based on belif networks. Only the type of ANN that is used for training changes.
The first significant work in the direction of solving this problem on the basis of artificial neural networks (ANN) is.5 In this dissertation, an attempt is made to solve the problem of increasing of images resolution (fingerprints) based on the frame processing of images by the Hopfield network. The widespread development of further research on the application of this type of ANN is based on the formulation of the problem of image super-resolution as a problem of soft classification13 of frames of images (for example, soil-vegetation cover) obtained by remote sensing. The main idea of the methods of this group is to maximize the spatial dependence of soil and vegetation frames and to maintain proportional information about the class of this cover. The soft classification provides the ability to produce a set of proportional images, each of which contains sub pixel information in a given class. Such information can be used as a source of additional information for increasing the detail and accuracy of the results of the image super-resolution methods, e.g for panchromatic images.14
However, these methods5,14 use the isotropic spatial model, which is based on the assumption that the spatial dependence of the classes of land cover is homogeneous and simplified if it changes with direction. Thus, the directions of the spatial sub pixel dependence of different classes (in this case, the soil-vegetation cover) are isotropic. This imposes a number of limitations on the accuracy of forecasting the boundary between classes, which may make it impossible to preserve the boundary forms of the region. In Thornton15 anisotropic model is used to eliminate this disadvantage. Despite the fact that the accuracy of these methods has improved, they can only be applied to specific classes of images (in this case, land cover). In Nguyen14 a universal approach is proposed. Apart from the fact that it is based on an anisotropic spatial model, it also uses the Sobel's operator to detect the magnitude and direction of the gradient. The direction of the gradient is used to determine the direction of the sub pixel spatial dependence. The gradient value is used to determine the weights of neighboring pixels in the system. The method is able to generate maps that are more accurate. This advantage becomes apparent when the resolution increase factor is large and the size of the partition window is greater 3*3 pixels. However, when changing the parameters of the method, the results of his work are unsatisfactory. The lack of the ability to determine automatically the parameters of the method does not allow its application in practice. In Dong16 another approach to solving a given problem is described. The method using a Convolution Neural Network (CNN), or a Dong's method, differs from existing ones, primarily because learning is done directly by matching pairs of low and high resolution images. The results of such training are displayed in the form of a Deep Convolution ANN. At the input of this method, an image of low resolution is presented, and an HR image is synthesized on the output.
The convolution ANN has a simple structure-3 layers. Each of them has its own functional purpose. The first layer performs the allocation of signs in the input image and represents each plot as a one-dimensional vector. The second layer non-linearly compares these vectors-signs with another set of vector-attributes that conceptually represent HR image frames. The third layer recombines these comparisons and synthesizes the original HR image. The method demonstrates good results in solving the problem of increasing the resolution of images and is characterized by high performance in application mode.16 However, this method has a number of shortcomings. It has been experimentally established that the quality of the images synthesized by this method depends to a great extent on the amount of the training sample. Since the training of such an ANN involves the use of the back-propagation of error algorithm and the increase in the training time shows the best results of synthesized images of elevated resolution according to the PSNR, this results in an extremely long, iterative learning process.17 In addition, this algorithm is characterized by a number of shortcomings (correct selection of the step, local minima, etc.), which imposes a number of restrictions on its use in applied problems of systems of technical vision, based on the principles of artificial intelligence.
In Tkachenko,18,19 the image super-resolution method based on the use of neural-like structures of the of Geometric Transformation Mode (NLS GTM) is developed. The peculiarity of this method is the non-iterative, fast learning procedure that takes place in only one pairs of images. The method involves preprocessing images, learning and applications. Preliminary processing is represented by a learning pairs of images in the form of a table of input/output, where the inputs represent frames of low resolution images, and outputs - high-resolution image frames. In Tkachenko,18 the best parameters of the NLS GTM were identified for solving the task. It is obvious that the methods of this group should be characterized by a high degree of generalization. One of the possibilities to ensure this is to increase the number of samples. In some cases Dong,16 this justifies itself. However, the use of a large training base (for individual methods) does not produce better results, since the presence of a large number of non-essential examples greatly affects the results of the method.19 Also, an increase in the training base increases the computing time when searching for the most probable samples to form the original image, which imposes a number of limitations when applying the method in real-time systems. Another disadvantage of these methods is that they do not guarantee that the true high-resolution parts of the image are obtained if the input frame contains textures that do not exist in the database.
Image super-resolution techniques based on the machine learning: experimental comparison
For the study, the most common methods for providing super-resolution are selected: Yang's methods, Zedeh; methods based on the use of gradient profiles, neural-like structure of the Geometric Transformations Model (NLS GTM) and a Convolution Neural Network (CNN); the classic method - bicubic interpolation. The parameters of the Yang's method are given in,9,10 gradient profiles – in.20 The training data for method based on the Convolution Neural Network, based on which the synthesis of high-resolution images was performed, is presented in.16 (Figure 2). The training of the image super-resolution method based on the NLS GTM occurred on a pair of images from Figure 3 (low-resolution image - No. 1, high-resolution image not shown). The parameters of the NLS GTM operation are given in.18 For an experimental comparison of the investigated methods, six different images are selected (Figure 2). Images in grayscale, two-byte, resolution-168*168 pixels. For a visual comparison of the work of various methods, in shows fragments of three times enlarged image №6 from Figure 2. As shown in Figure 3, the best results are obtained for an image enhanced by a method based on a Convolution Neural Network. This is confirmed by increasing all other images of the test sample.

Figure 3 Fragments of an enlarged three-dimensional image No. 6 (from Figure 2), different methods.
In Table 1 shows the Peak Signal to Noise (PSNR) ratio for enlarged test sample images. The value of PSNR for all images has confirmed the high efficiency of using the method based on the Convolution Neural Network to provide HR images.
| Image # | Bicubic | Yang's | Zedeh's | Gradient | NLS GTM Method | CNN Method |
| 1 | 322,087 | 322,087 | 331,987 | 331,987 | 331,221 | 341,431 |
| 2 | 316,118 | 316,218 | 316,219 | 31,8 | 311,465 | 324,996 |
| 3 | 234,473 | 234,473 | 234,474 | 23,81 | 232,548 | 239,121 |
| 4 | 274,614 | 274,614 | 274,615 | 28,4 | 268,106 | 289,483 |
| 5 | 320,252 | 320,256 | 320,257 | 32,94 | 310,665 | 330,799 |
| 6 | 267,048 | 267,051 | 267,052 | 27,3 | 263,758 | 27,73 |
Table 1 PSNR for enlarged thirty images by various methods
The review of literary sources, a classification of basic methods for image super-resolution in the case of one input image is proposed. Within this framework, the advantages and disadvantages of modern methods of providing image super-resolution based on machine learning are highlighted. It is established that the process of increasing the resolution of images by methods based on the technology of reconstruction, is accompanied by the blurring of contours that determine homogeneous areas of objects in images, and therefore necessitates the use of post-processing procedures. It is revealed that the main disadvantage of some methods based on learning is the inability to work on small-dimensional samples. This imposes additional conditions on the dimension of the training sample, namely the need to provide a large set of training data and, accordingly, increase the computational burden in the learning process. The iterative learning algorithms that are implemented based on ANNs do not provide sufficient computational speed, which in turn imposes restrictions on their application in practical systems of artificial intelligence based on the principles of technical vision. The decisive feature of the methods of this class is the high computational complexity, which highlights the high requirements for hardware and software. Therefore, the actual task is to lower the computing costs while preserving the quality of re-imaging images while solving the problem of providing super-resolution images.
No financial interest exists.
No conflict of interest exists.
Machine Learning for Different Resolution Pictures
Source: https://medcraveonline.com/IRATJ/image-super-resolution-techniques-based-on-machine-learning-comparative-review.html